Part One:
Here Comes a Sun
Today's assignment is in the Thermal Defense Room. This room serves as the ship's primary defense against the unforgiving natural perils of space — extreme heat and harmful radiation.
In space, the ship is constantly bombarded with waves of different frequencies and wavelengths. Some of these waves, called Solar Waves, are damaging to the structure of the ship, while others, called Cosmic Waves, are harmless.
The ship has a Thermal Defense System in place, but it works best when it is specifically targeted at harmful Solar Waves.
A comma-separated database is already on file, containing the individual frequencies and wavelengths of previously intercepted waves. However, some incoming waves have a combination of frequency and wavelength that has not yet been classified.
Your job is to determine if these waves are harmful Solar Waves or harmless Cosmic Waves. To do so, you need to find the 7 known waves from the database that are nearest to the unknown wave.
The distance between waves is determined by graphing the coordinates, with frequency representing the x-axis and wavelength representing the y-axis.
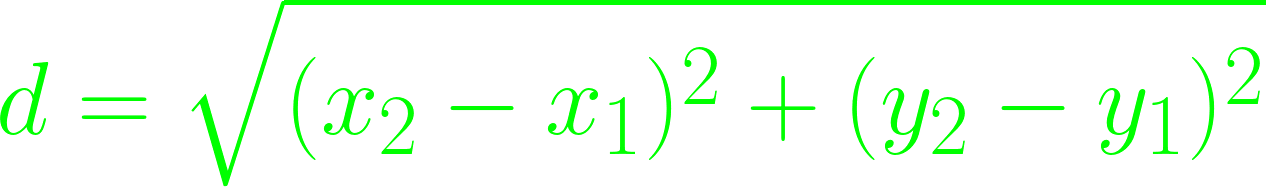
The data provided, your puzzle input, begins with a single line of new waves, with each wave represented by its frequency and wavelength separated by a comma; the individual waves are separated by spaces. The following several lines, in comma-separated format, provide a database of known waves. In this format, the first column is "frequency", the second column is "wavelength", and the third column is "type". Determine whether each new wave is a Solar Wave (S) or a Cosmic Wave (C), and concatenate these results without spaces into an uppercase five-character output.
For example:
If your unknown waves are (9,2) (6,4) (3,5)
and
your database consists of
frequency,wavelength,type
10,7,Cosmic
9,1,Solar
7,2,Solar
8,3,Cosmic
10,2,Solar
9,3,Solar
1,5,Cosmic
4,5,Cosmic
9,4,Solar
3,3,Solar
To find the distance from the first unknown wave (9,2) to the first wave in the database
(10,7), you would apply the Euclidean Distance Formula, taking the square root of the sum
of the difference of the Xs squared and the difference of the Ys squared:
√( (10-9)² + (7-2)² ) = √( 1² + 5² ) = √( 1 + 25 ) =
√( 26 ) = 5.099
So the distance between the first unknown target wave and the known Cosmic Wave at (10,7) is 5.099
Applying this formula to every wave in the database you get:
frequency,wavelength,type,distance
10,7,Cosmic,5.099
9,1,Solar,1.000
7,2,Solar,2.000
8,3,Cosmic,1.414
10,2,Solar,1.000
9,3,Solar,1.000
1,5,Cosmic,8.544
4,5,Cosmic,5.830
9,4,Solar,2.000
3,3,Solar,6.082
Since you have such a small amount of data in this example, let's only look at the
3 nearest neighbors. Those would be
- Solar Wave at (9,1)
- Solar Wave at (10,2)
- Solar Wave at (9,3)
Repeating the same process for all the unknown waves, you get
- for (9,2): Solar, Solar, Solar = S
- for (6,4): Cosmic, Cosmic, Solar = C
- for (3,5): Cosmic, Cosmic, Solar = C
